What do all the lines and boxes mean on a boxplot?

The Boxplot is one of simplest graphical tools to look at, and a tool I use very frequently when first reviewing my data sets. It is a great visual tool for showing the variation and average of a data set, that is not sensitive to outliers (nonparametric approach). The chart shows how the data breaks down by categories, to help you identify areas of concern or potential causes of your problem.

However, it is the most confusing chart to explain how each piece of the box is calculated. When teaching a basic statistics class, I actually avoid discussing the boxplot, because it brings about many questions and becomes a distraction for the class attendees.

When we look at the boxplot simplistically, it gives us a quick understanding of our data. Let’s look at an example from Minitab.

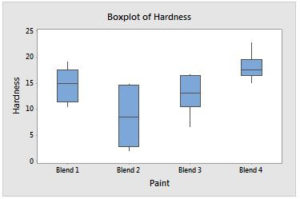
You should be able to draw some simple conclusions from the chart

• The boxplot for the paint data shows that paint blend 4 has both the highest median and least variability, with an interquartile range of only 3.10.
• Blends 1 and 3 appear to have roughly similar medians and variability.
• Blend 2 has the lowest median and greatest variability, with an interquartile range of 11.72. The short whiskers indicate clumps of data near the box endpoints.
• There are no outliers in the data

Ultimately, the very next question is always “how are the box and lines calculated?”

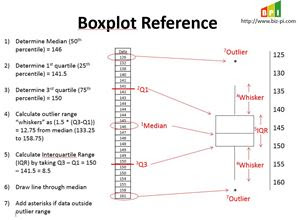
Let’s breakdown the chart to help clarify it.

1. Determine Median (50th percentile) = 146
2. Determine 1st quartile (25th percentile) = 141.5
3. Determine 3rd quartile (75th percentile) = 150
4. Calculate outlier range “whiskers” as (1.5 * (Q3-Q1)) = 12.75 from median (133.25 to 158.75)
5. Calculate Interquartile Range (IQR) by taking Q3 – Q1 = 150 – 141.5 = 8.5
6. Draw line through median
7. Add asterisks if data outside outlier range

You can also download the Boxplot guide below for future reference.

Hopefully this helps you understand box plots, and you see the need to use them prior to analyzing any data set.