How the Tukey Method test in Minitab adjusts treatment means when using ANOVA with covariates

After digging into the manual calculations of the Tukey test to compare group averages, another observation was made that I couldn’t quite understand.

If you add a covariate (continuous input variable) into the ANOVA analysis, then perform the Tukey test, the group means will change, which could change which groups are determined to be different or similar. Why? I wasn’t quite sure, so I did some more research and wanted to share what I found.

Let’s back up, what is a covariate?

Typically in an Analysis of Variance (ANOVA), we use continuous output data with categorical input data.

An example is a data set I found (Time to Pain Relief by Treatment and Sex – Clinical Site 2) that I modified with an additional field (Room Temp). You can download the data set here (XLSX).

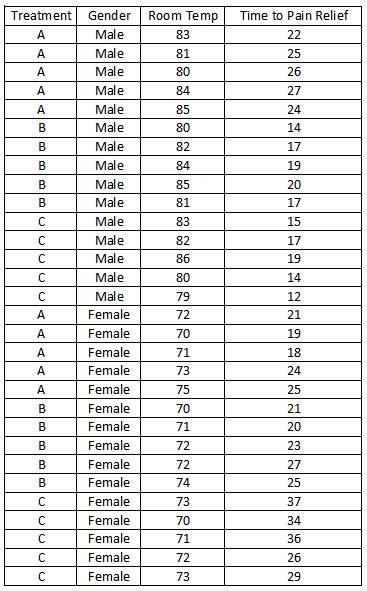
In this data, “Time to Pain Relief” is the output (dependent variable), which is continuous. For the process inputs (independent variables), the categorical factors are “Treatment” and “Gender”, along with one continuous input factor, “Room Temp.”

In Minitab, you can run a General Linear Model (GLM) using ANOVA for the categorical factors. However, it also allows you to add a covariate, which is used for continuous inputs. This analysis would be called an Analysis of Covariance (ANCOVA). This allows us to perform an analysis using different types of input factors, which makes it very flexible. You can also run a Regression Analysis with categorical and continuous input factors, but Minitab does not allow you to perform a Tukey test from a Regression, so we’ll stick with ANOVA / ANCOVA for this article.

Let me show you the problem. First, let’s look at some simple summary statistics before any analysis is performed.

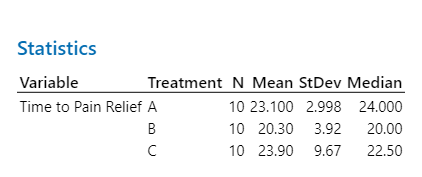
If I run an ANOVA and Tukey test with Output = Time, and Inputs = Gender and Treatment, here are the results:

Regression Equation: Time to Pain Relief = 22.433 + 0.67 Treatment_A – 2.13 Treatment_B + 1.47 Treatment_C + 3.233 Gender_Female – 3.233 Gender_Male

As you can see, the summary statistics match the Tukey Method group means for each level within each factor.

When we run the ANCOVA by adding in Temp as a covariate, we can see some expected and unexpected changes in the output.

When adding more factors to the analysis, I’m not surprised that the R-squared improves, along with the reduction in the mean square error (S), as adding a significant factor will always do that. However, the group means for the Tukey test are now different, which is what started this investigation. Here is a summary table of the differences when using the covariate variable.

I wanted to figure out how Minitab adjusts the means when a covariate (Room Temp) is included (ANCOVA), compared to when it is not included (ANOVA).

To summarize why this happens, the covariate effect is calculated as a slope (like a correlation between the continuous output and the continuous input).

Based on the slope, there is an offset made to the values to account for that slope. When you remove that variation from the results, you can more appropriately compare the difference in the categorical factors.

This is done by making the following adjustment to the Y (output) values for “Time to Temp” (converting it to a new value, we’ll call Z)

To determine the beta (B) value, we’ll run two ANOVA (GLM) analyses:

ANOVA #1: Output (Y) = Time to Relief, Inputs (X) = Treatment and Gender
ANOVA #2: Output (Y) = Room Temp, Inputs (X) = Treatment and Gender

The residuals from that analysis will be stored into the Minitab worksheet, and one more analysis will be run, a Regression Analysis comparing the two residuals. The Regression equation will contain the B value (see below).

ANOVA #1

Regression Equation: Time to Pain Relief = 22.433 + 0.67 Treatment_A – 2.13 Treatment_B + 1.47 Treatment_C + 3.233 Gender_Female – 3.233 Gender_Male

ANOVA #2

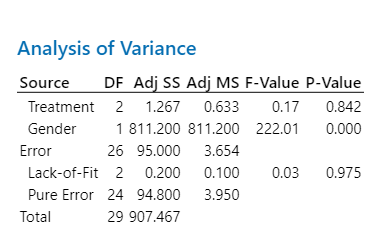
Regression Equation: Room Temp = 77.133 + 0.267 Treatment_A – 0.033 Treatment_B – 0.233 Treatment_C + 5.200 Gender_Female + 5.200 Gender_Male

Residuals

Here are the first few rows of the two sets of residuals generated from the ANOVA analysis.

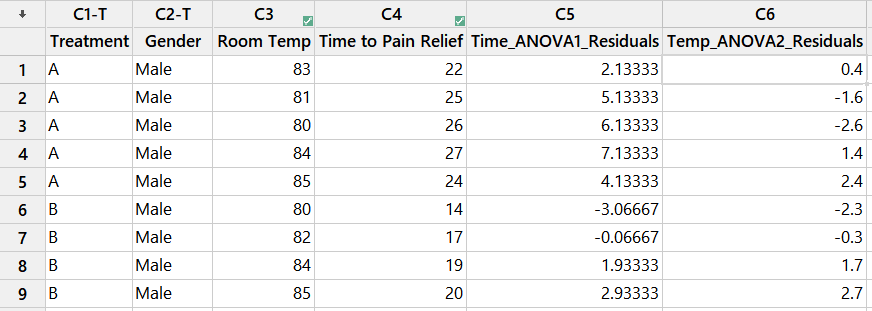
Next, we run a Regression Analysis between the two residual columns

Regression: Y = Time_ANOVA1_Residuals, X = Temp_ANOVA2_Residuals

Where B = 0.785

Next, we’ll adjust the Y value using the formula below, to convert it to Z (Calculation column for the Adjusted Mean)

The adjustment will be done on the means of each level. In the formula, X will be the group mean of each level for Temp, Y is the current Time to Relief, and X-bar will be the overall average of Room Temp, which is 77.13.

As you can see, these new calculations now match the Tukey mean data in the results above.

Hope you found that helpful!